Вспомним: Привычные комбинаторные объекты мы умеем считать Перестановки:
Сочетания: Скобочные последовательности: и тд
Рекурентные соотношения и динамическое программирование
Сочетания (под другим углом)
Перестановки
Правильные скобочные последовательности (п.с.п.)
префиксы - неотрицательный баланс - в конце баланс
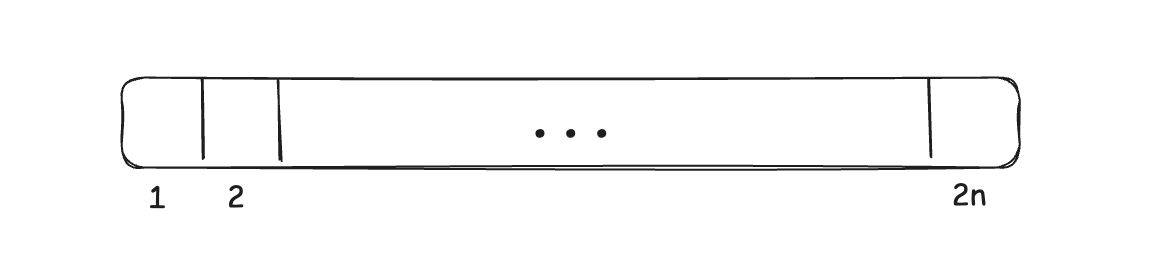
Без требования 1) -
Но нам нужно ещё и выполнение условия 2)
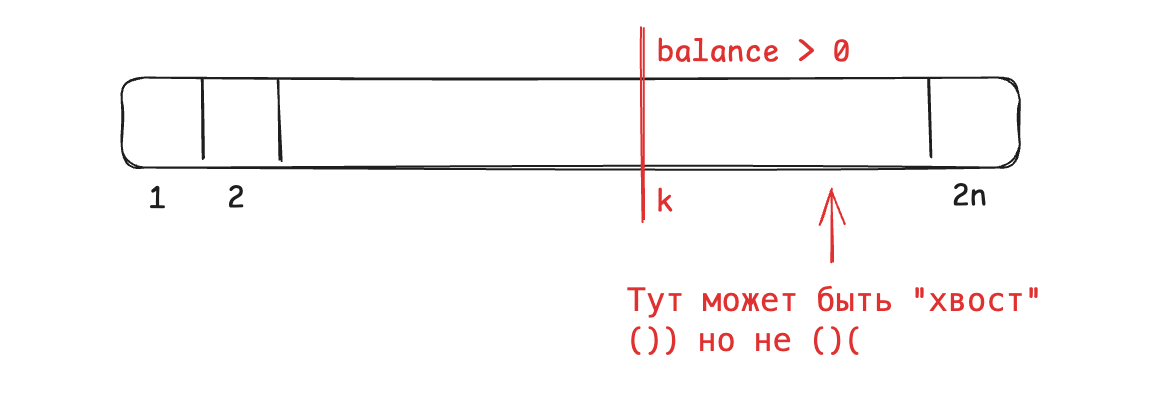
На базе этого придумаем формулу:
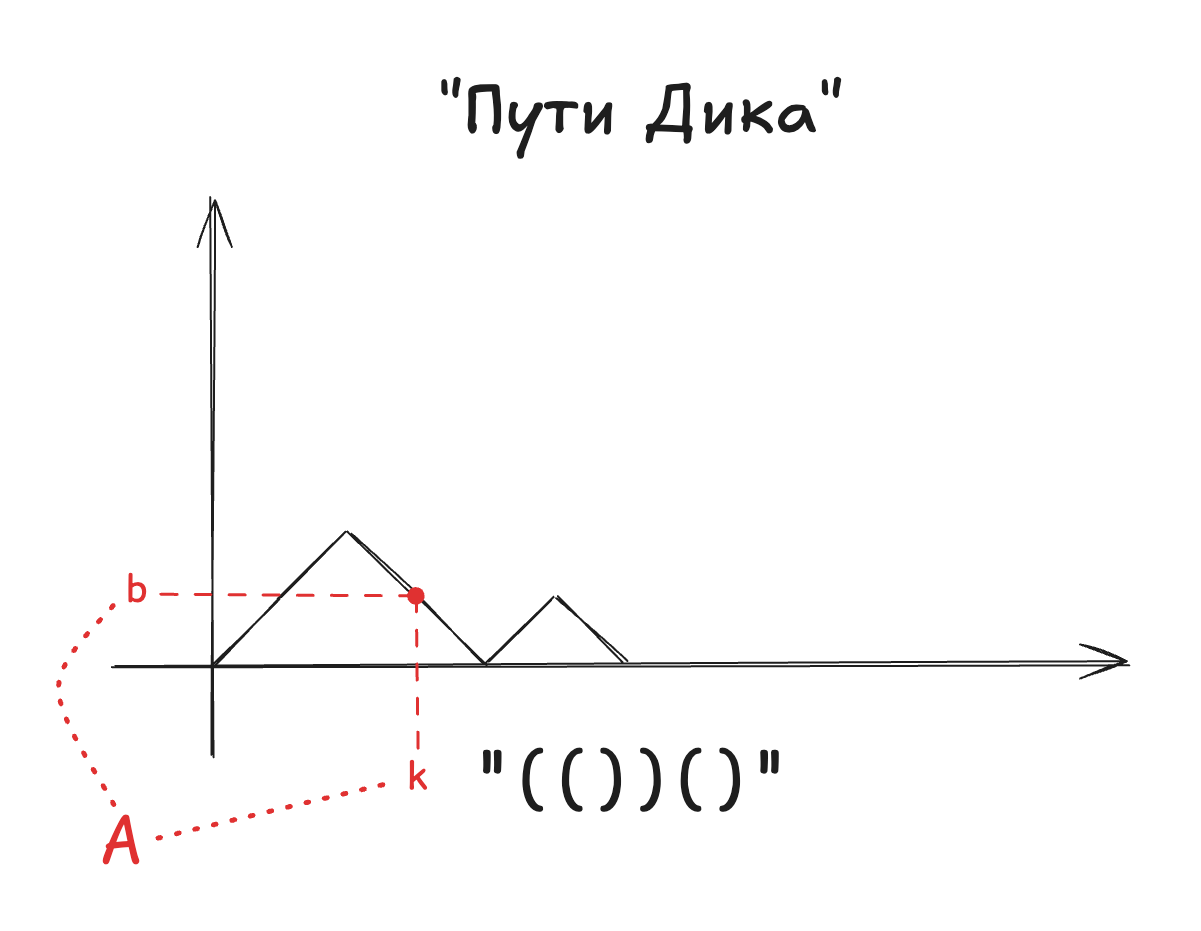
- На первом месте очевидно
- На последнем очевидно
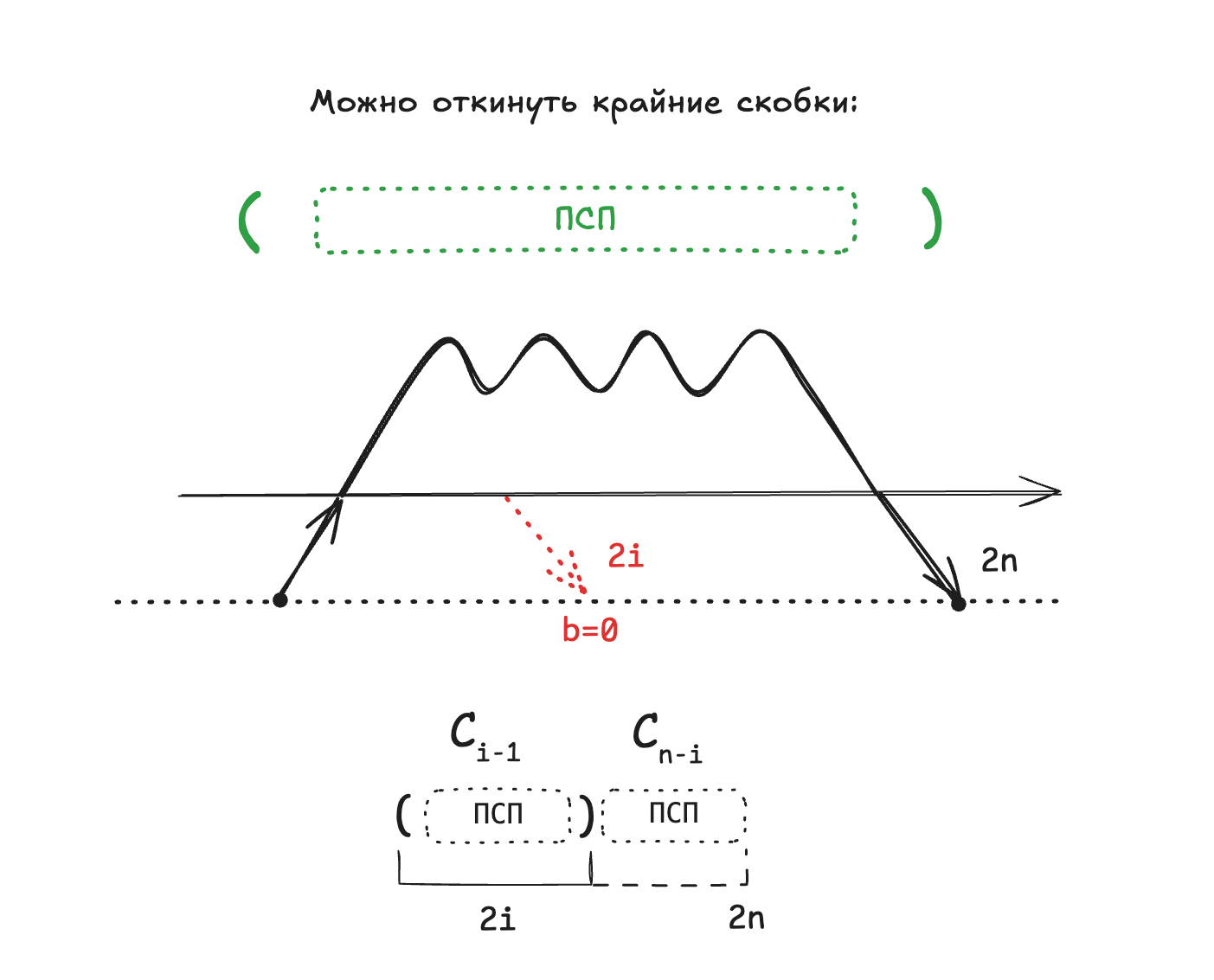
Двоичные деревья
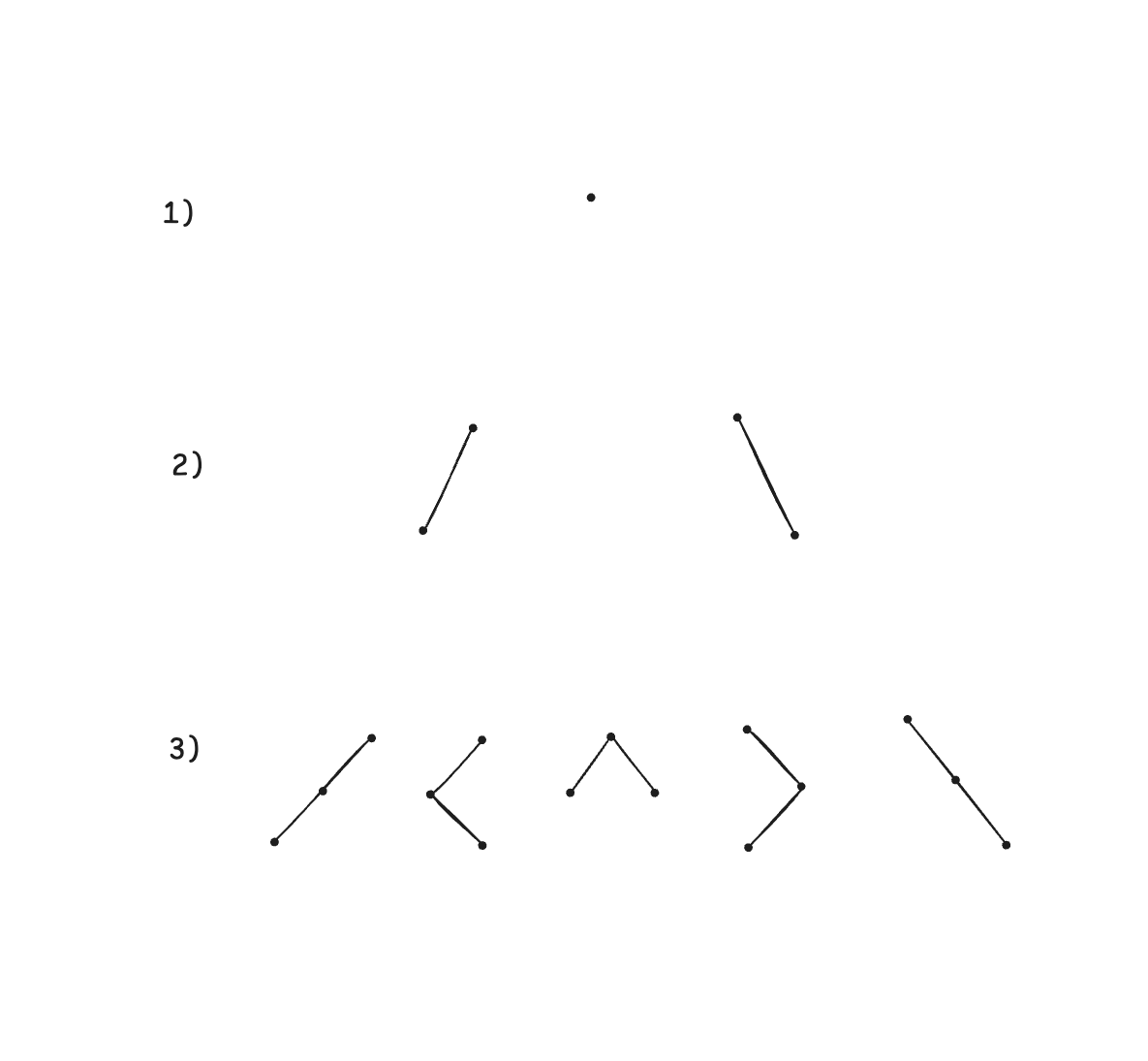
Разбиения
Диаграмма Юнга (Ферре)
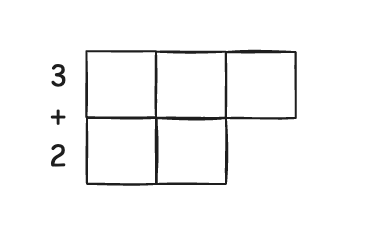
Каноническое представление
Слагаемые представлены по убыванию
| 0 | 1 | 2 | 3 | 4 | 5 | |
|---|---|---|---|---|---|---|
| 0 | 1 | 1 | 1 | 1 | 1 | 1 |
| 1 | 0 | 1 | 1 | 1 | 1 | 1 |
| 2 | 0 | 1 | 2 | 2 | 2 | 2 |
| 3 | 0 | 1 | 2 | 3 | 3 | 3 |
| 4 | 0 | 1 | 3 | 4 | 5 | 5 |
| 5 | 0 | 1 | 3 | 5 | 6 | 7 |
Теперь шары пронумерованы
Число Белла
Количество разбиений
| 0 | 1 | 2 | 3 | 4 | |
|---|---|---|---|---|---|
| 0 | 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 | 0 | 0 |
| 2 | 0 | 1 | 1 | 0 | 0 |
| 3 | 0 | 1 | 3 | 1 | 0 |
| 4 | 0 | 1 | 7 | 6 | 1 |
Разбиения на циклы
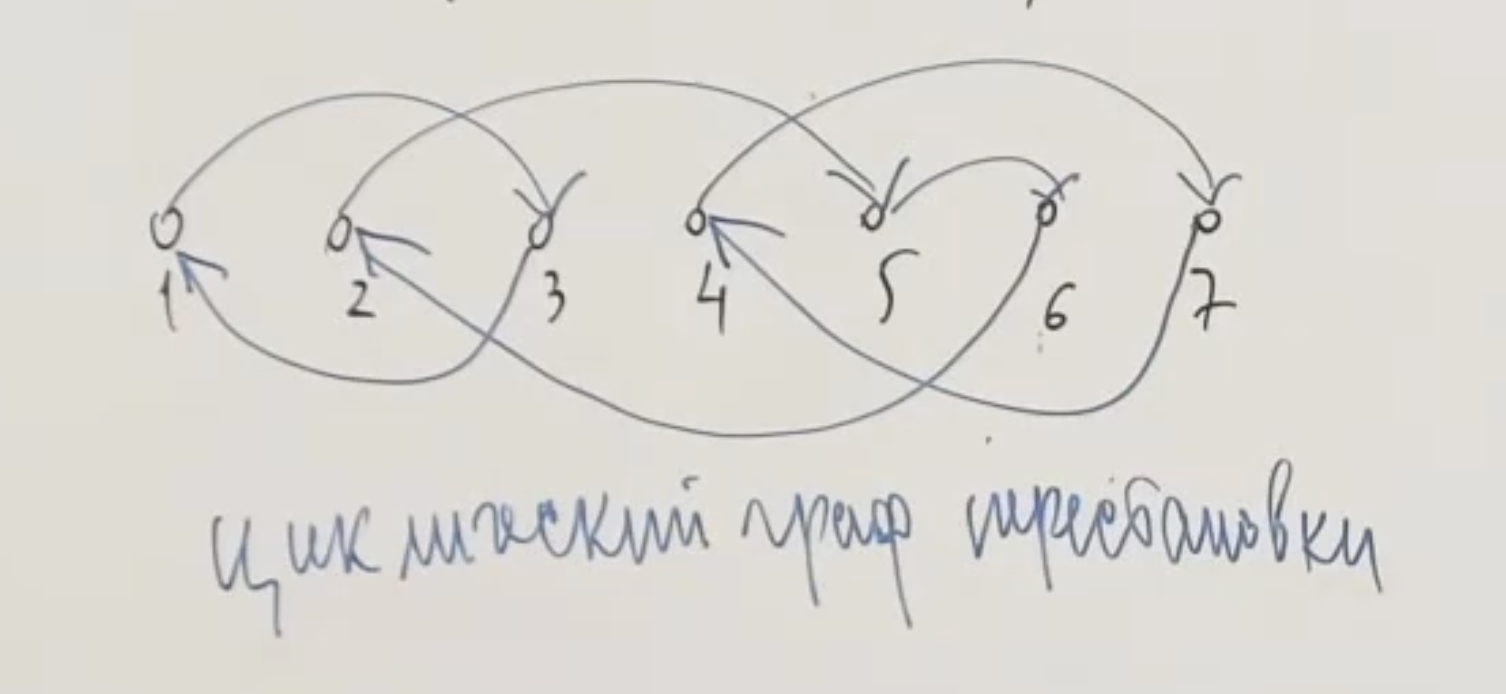
Число Стерлинга первого рода
| 0 | 1 | 2 | 3 | 4 | |
|---|---|---|---|---|---|
| 0 | 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 | 0 | 0 |
| 2 | 0 | 1 | 1 | 0 | 0 |
| 3 | 0 | 2 | 3 | 1 | 0 |
| 4 | 0 | 6 | 11 | 6 | 1 |