Группы Действий, Леммы Бернсайда, Формула Пойа

Размещения

"Массив" из упорядоченных элементов:

Сочетания

"Набор" из неупорядоченных элементов:

На размещениях введём отношение эквивалентности: Массив , массив () Отношение - равенство с точности до порядка

Группа

Группоид:

Полугруппа:

Моноид:

Нейтральный элемент:

- обратное действие есть

- обратного действия нет

Группа:

Моноид, у которого есть обратный () элемент

Группа действий

- группа

- объект

"дейстует" на

Пример 1:

Пример 2:

Пример 3:




Умножение перестановок = действие на

Пример 4: "Циклические сдвиги"

- группа действует на
Введём - отношение эквивалентности ("равны с точностю до G"):

3. , где

- классы эквивалентности (орбиты)

Массивы с точностью до циклического сдвига (пример 4) называются "ожирелья"

Неподвижные точки

В перестановке - элементы циклов, в которых все элементы равны В сдвиге - (сдвиг равен длине) Число циклов =

Лемма Бернсайда

Доказательство:

- размещения - перестановки

- сочетания

- классы эквивалентности зависят только от количества единиц

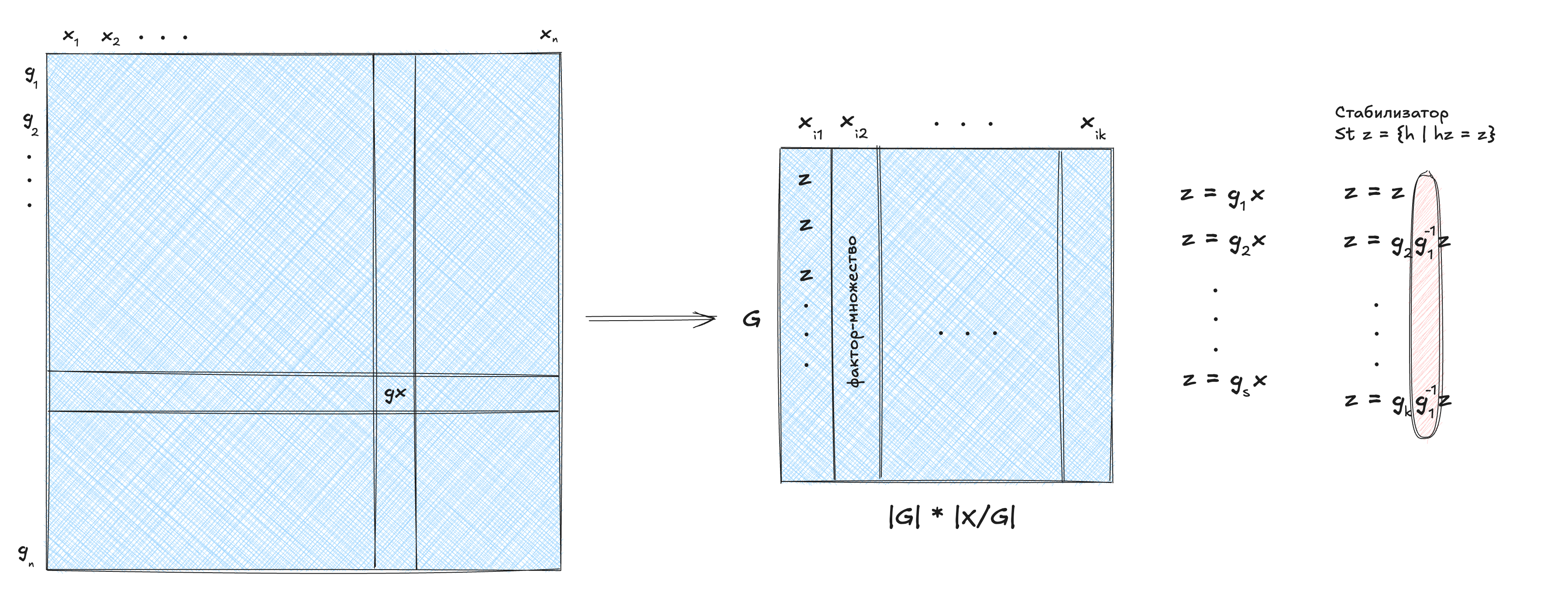
Ожирелья

Теорема Пойа

- группа
(Циклический сдвиг )