Обзорно по побитовым операциям:

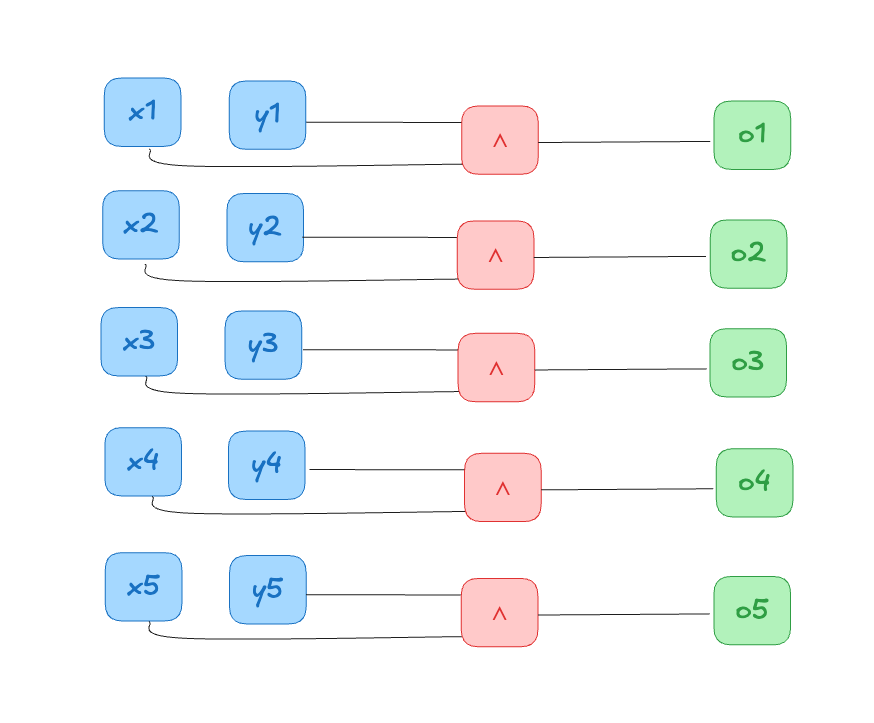
Побитовое "и" - схема из функциональных элементов

С остальными операциями также

Сумматоры

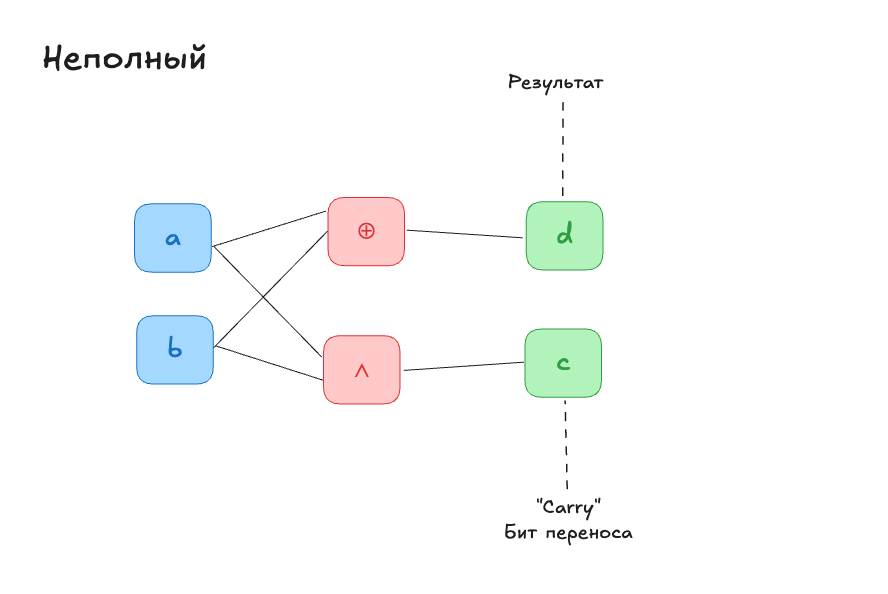
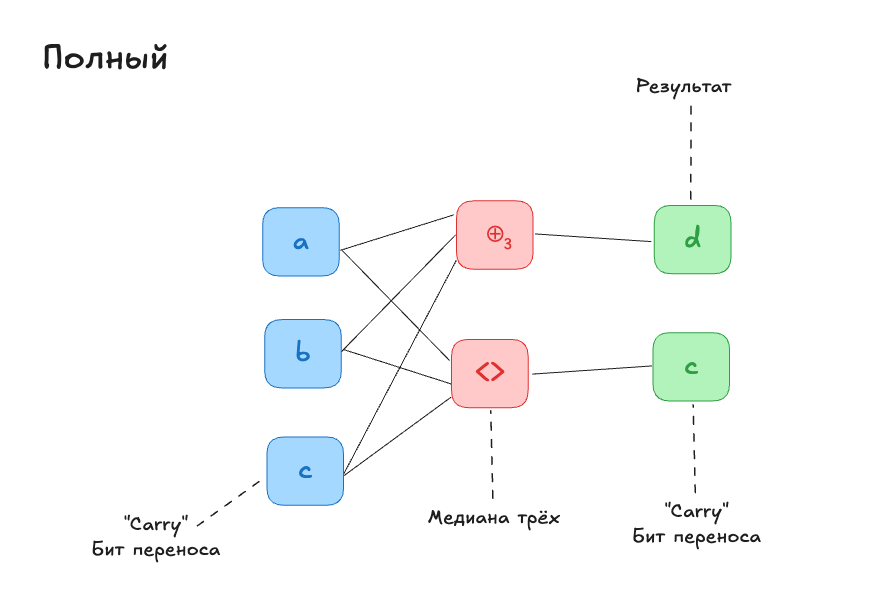
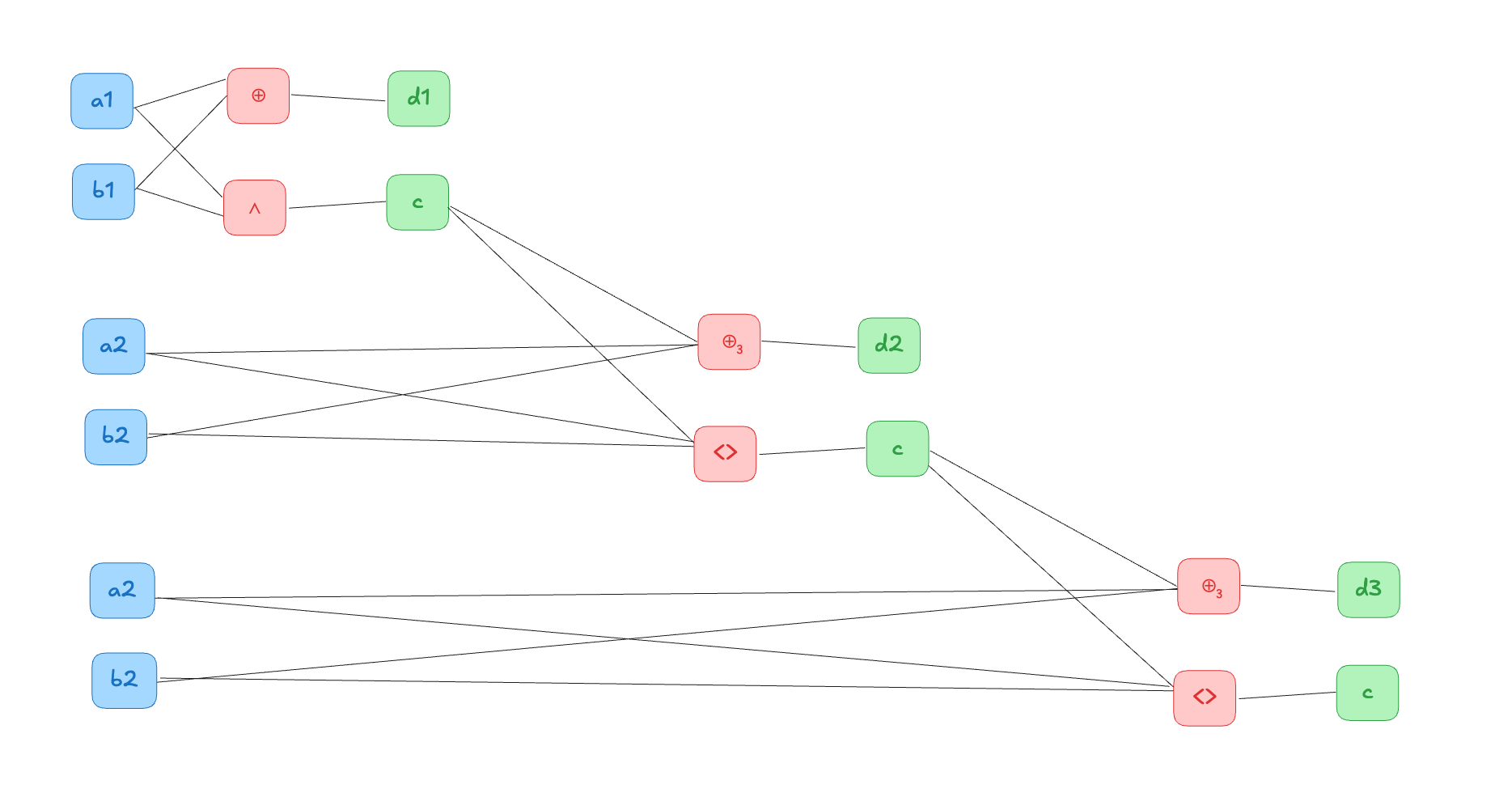
Адекватный сумматор трёхбитного числа (поразрядный)

Где это количество бит

Сумматор построенный на рисунке выше называется каскадным от слова "cascade".

Неприятно что , хочется сделать за так что

Абстрагируемся от сложной задачи и подумаем, о том, когда бит переноса точно , а когда точно . Намеренно не включим бит переноса с предыдущего разряда, чтобы уследить зависимость от него:

Получается, наш сумматор с точки зрения функции относительно предыдущего бита переноса, принимает всего 3 значения (этим значениям даже придуманы названия):

• - kill - сумма двух нулей и у нас 100% не будет бита переноса дальше, даже если он пришёл с предыдущего разряда
• - propagate - сумма разных значений; если нам пришёл бит переноса с предыдущего разряда, он же пойдёт в бит переноса у нас: если не пришёл, будет 0
• - generate - сумма двух единиц и у нас 100% будет бит переноса, даже если нам он не пришёл с предыдущего разряда

Представим что мы делаем композицию двух функций описанных выше, то-есть смотрим на входы двух сумматоров и пытаемся понять, если сумматор "пропустит через себя" бит переноса (we try to determine if the device will propagate the carry bit), или выдаст предетерменированный результат ().

Рассмотрим таблицу композиции функции (1 - первая операция, 2 - вторая):

- нейтральный элемент, коммутативности нет, ассоциативность есть (так сказал А.С. Станкевич, я ему верю)

Эту функцию композиции отобразим схематично, для тех кто ещё не врубился что тут происходит:

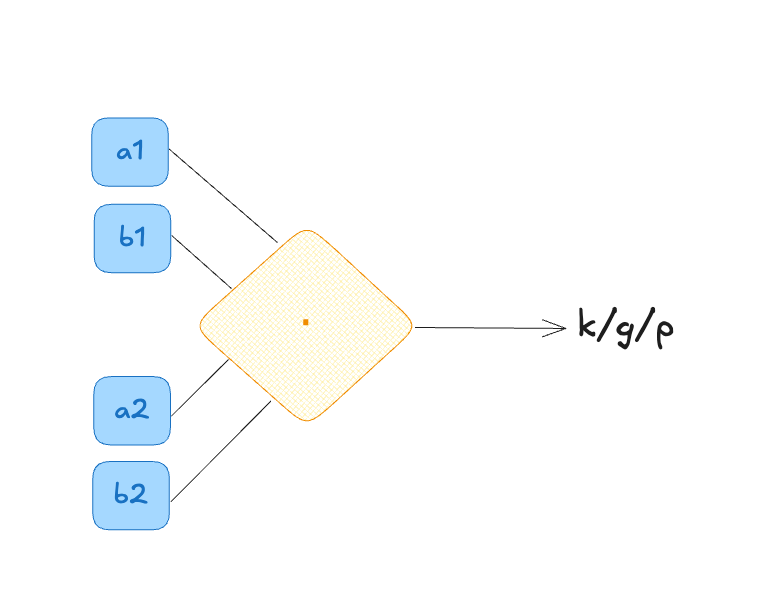Выше, - аргументы одного сумматора, - аргументы второго.

Композиция этих функция говорит, если этот участок из двух разрядов при сложении переопределяет бит на что-то детерменированное, или пропускает то что шло до него.

Мы можем масштабировать эту систему, чтобы выяснить как ведёт себя вся совокупность из бит (разрядов), чтобы вычислить все биты переноса за глубину .

Ниже приводится схематика того, как это работает.

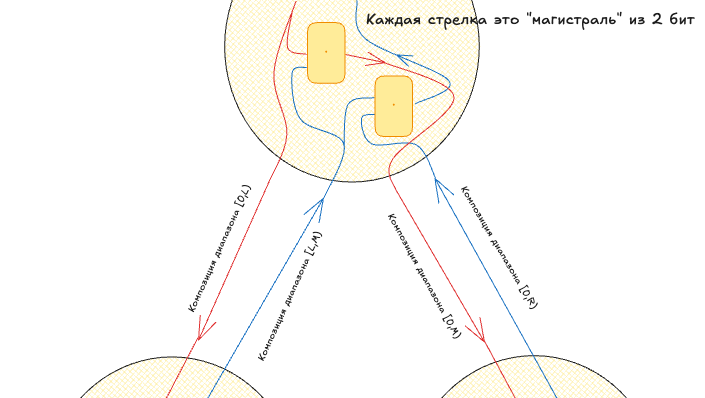
Недеюсь этот конспект используют достаточно человек чтобы оправдать время на рисование этой схемы...