Для почти всех функциональных элементов

При том для всех схем которые известны:

Возьмём базис

Берём функцию

функциональная программа

• Состоит из строчек
• -ая строка имеет номер
• 
  
  

Теорема

в имеет л. п. из строк имеет схему из ф.э. содержазщую элементов

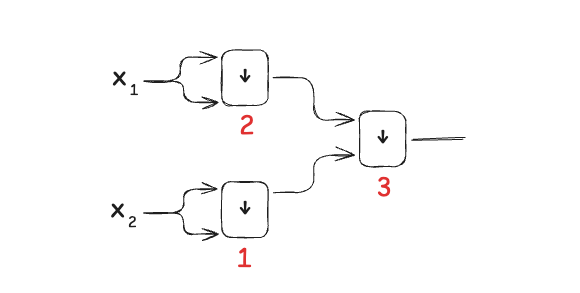
Заметим что у одной схемы может быть несколько линейных программ

В схеме выше мы поменяли местами ноды и

У разных схем разные линейные программы

Если то схем размера достаточно, чтобы задать функций

для большинства схем нужно хотя бы элементов

Теорема ( нижней оценке)

то схем размера достаточно, чтобы задать функций

Теорема (о верхней оценке)

булевой функцкии от аргументов схема из ф.эл., содержащая элементов

Обзовём последних аргументов функции чушпанами
Составим таблицу истинности вида:

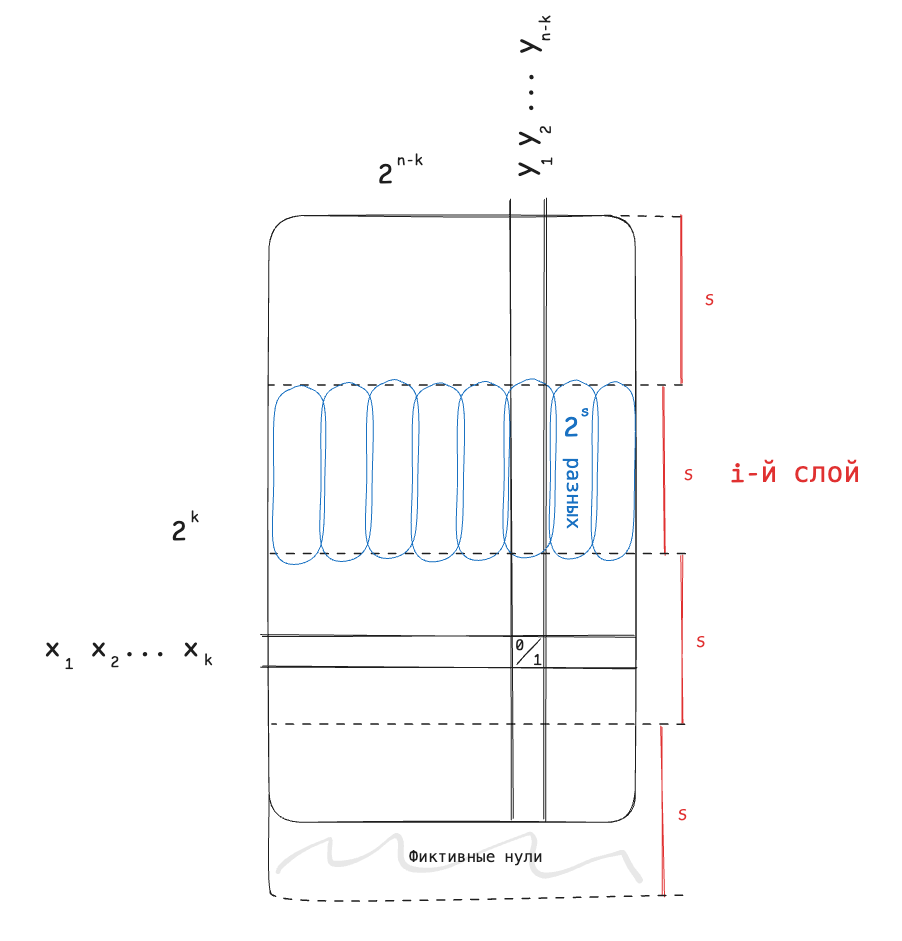
Кол-во слоёв:

Рассмотрим столбцы (сининькие), их можно придумать разных (бинарные)

Тип маски столбца , -го слоя (просто число):

- маска В -м слое маска , а снаружи нули:

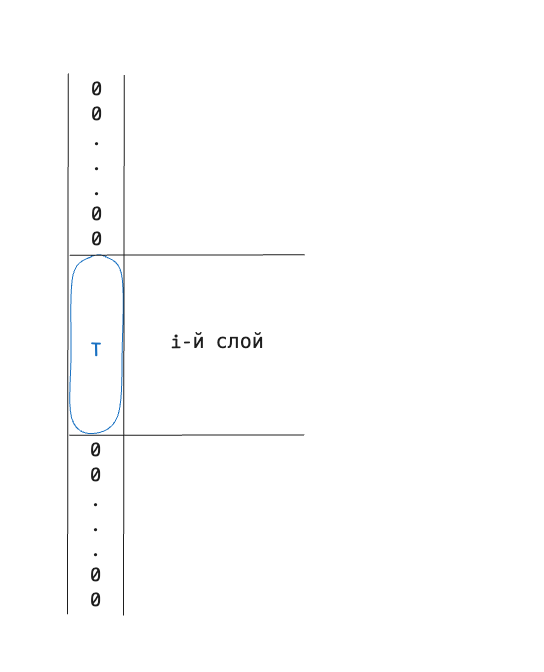
функция с таблицей истинности выше

*тут rage quit по восприятию*

САМОЕ ВАЖНОЕ

1. Схемная сложность почти любой функции
2. Метод подсчёта для нижних оценок важен