, над




сюръективен

Теорема

столбцы - базис



в
в

над

Определим операции над гомоморфизмами

- нейтральный элемент

- векторное пространство

Утверждается что пространства изоморфны:

Гомоморфизм:

Биекция:
- изоморфизм

-тая векторная координата образа




- умножение матриц и
умножение матриц ассоциативно, т.к. композиция ассоциативна

- подпространство ?

Пример:

В общем случае нет!

Сумма подпространств

- наименьшее подпространство и
- наибольшее подпространство содержащееся в и

Теорема Нётер об изоморфизме

Доказательство:

- каноническая проекция Ограничиние на -

У есть прообраз

По осн. теореме

Следствие (формула Грассмана)

Доказательство:

Следствие

линейно независимые, если

Частный случай

линейно независимы
линейно завсимы

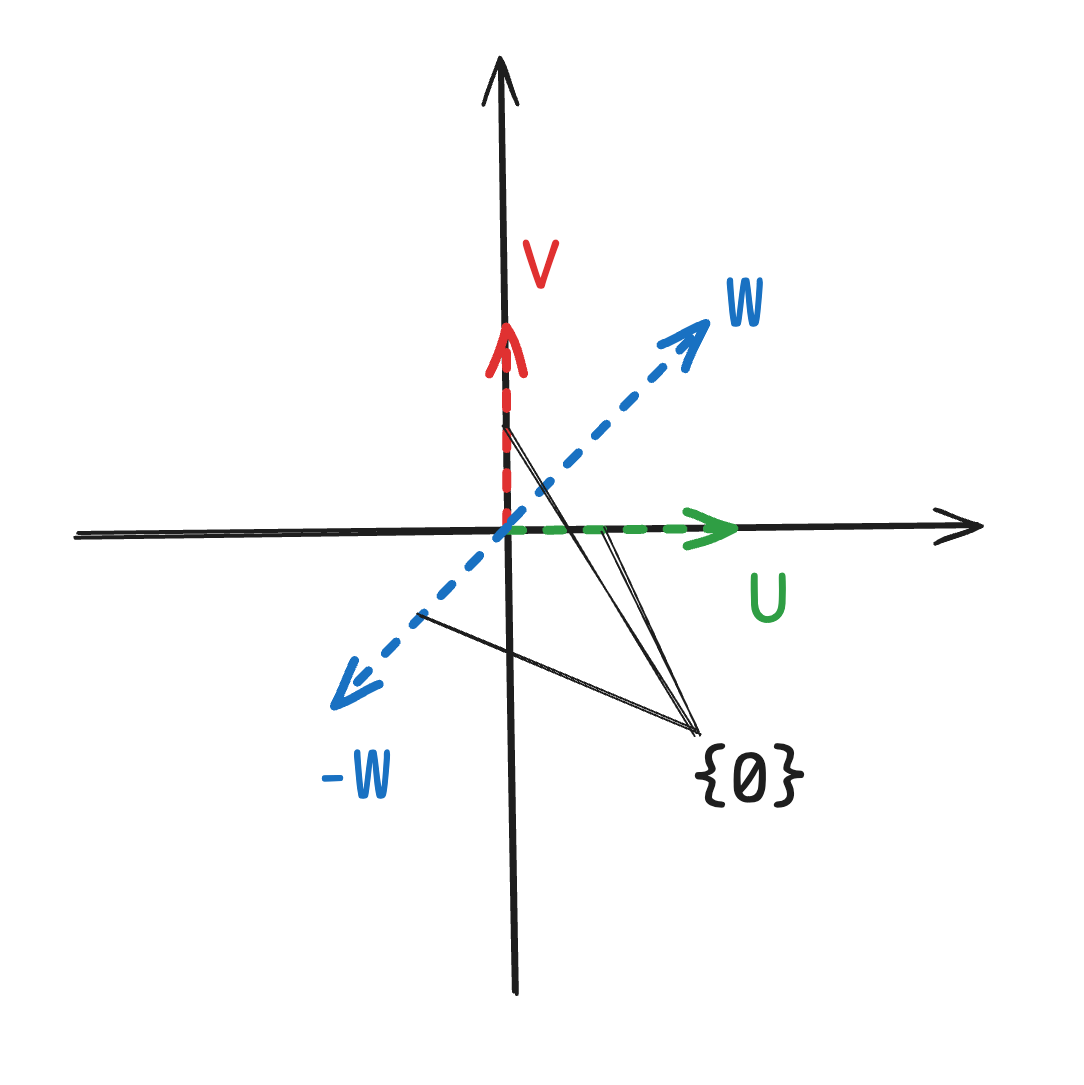
Два пространства линейно независимы

Пример:

Лемма

Следующие условия эквивалентны:

1. - линейно независимы
2. Объединение их базисов линейно независимо

Доказательство:

- базис
Объединение базисов

Пусть нетривиальная линейная комбинация
Перегруппируем хотя-бы один линейно зависимы

есть в его разложении по базису есть не нули объединение базисов линейно зависимо

, если , то

Внутренняя прямая сумма

2. линейно независимы

Пример:

1. (внешняя прямая сумма подполей) В
2. (линейная независимость)

- векторные пространства над

Внешняя прямая сумма

(канонический изоморфизм)

Пример:

2. линейно независимы
   
   дополнение к
   
   

Проекция зависит не только от пространства на которое проецируем, но и от дополнения

Пример: - базис

Пример:

1. 
   
   
   
   
   
2. (линейная независимость)
   

Пример:

Базис и размерность

Базис и размерность и
Каждое подпространство задаём с помощью однородной СЛАУ