Пример:
1.



2.

Пример:

Пример:

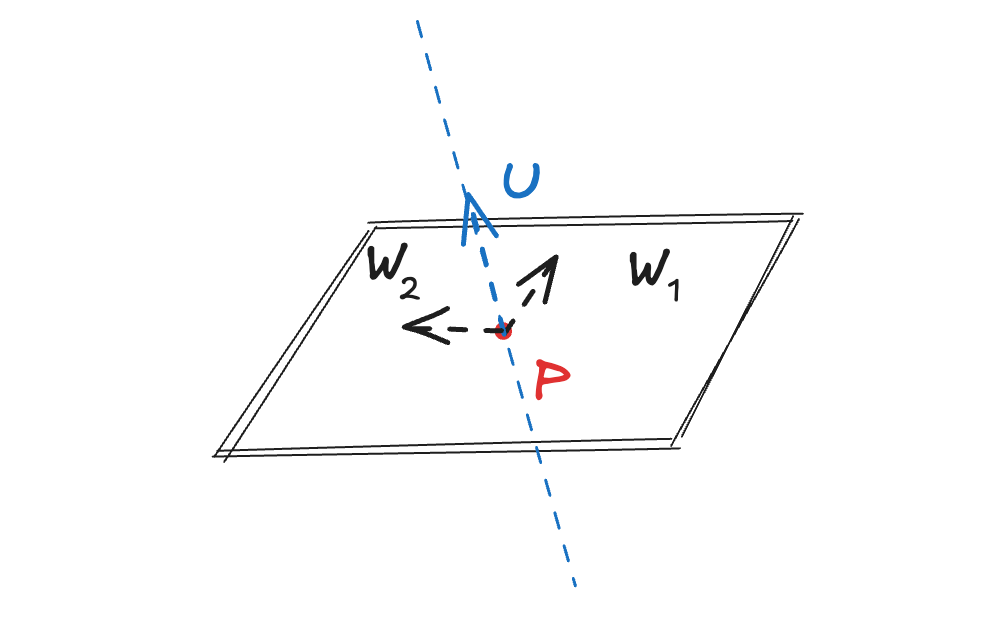
Аффинизация

"концы радиус-векторов"

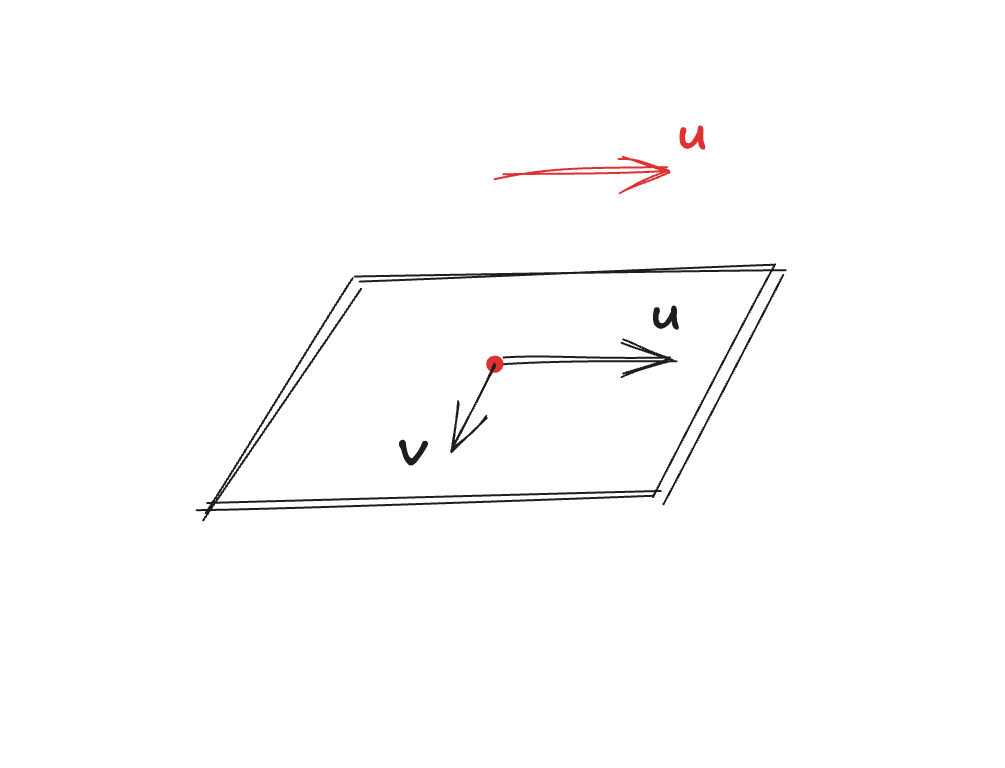
Векторизация

Начало отсчёта
Точки

Барицентрическая комбинация точек
Выберем
Что если ?

Материальная точка

Пара

Центр масс системы материальных точек

- точка




барицентрическая комбинация

Так определённый центр масс соответствует физическим представлениям о нём в вещественном пространстве

1. Для любой системы материальныэ точек, центр масс
2. Удовлетворяет правилу рычага
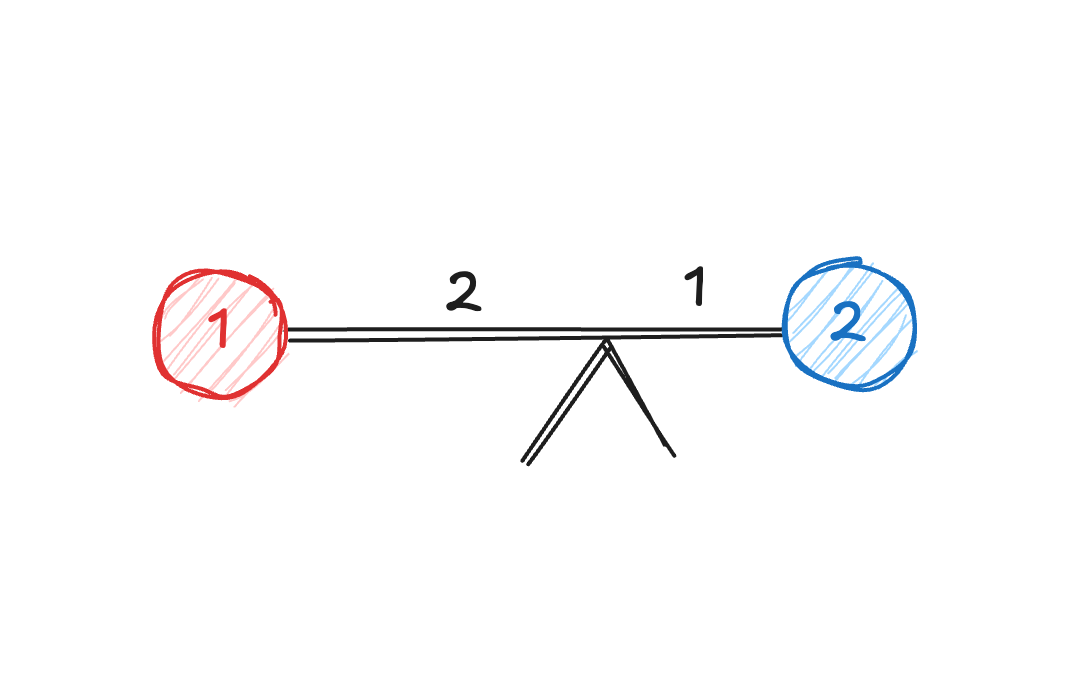
3. Центр масс не меняется при замене некоторых точек на их материальный центр - барицентрическая комбинация
   Пусть - начало отсчёта
   
   - середина точек и
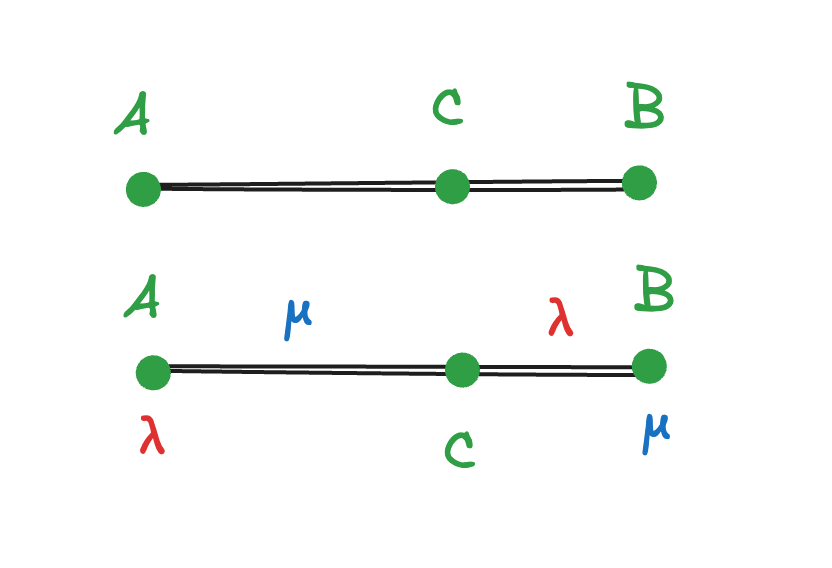
   (привычная середина отрезка)

Теорема о группировке масс

Центр масс системы материальных точек не изменится, если некоторую её подсистему заменить на материальный центр

Доказательство

Возьмём в качестве начала отсчёта точку

Точка - центр масс системы материальных точек

- барицентрическая выпуклая комбинация

Пример:

- множество всех выпуклых комбинаций - выпуклая оболочка

Выпуклая фигура
если , то и

в мерном пространстве и не лежат в гиперплоскости (размера ) мерный симплекс

Пример мерных симплексов: точка - отрезок треугольник тетраэдр

Факт (Теорема Хелли)

Если любые из них имеют общую точку, то все фигуры имеют общую точку

Пример:

- векторное пространство

группа
- левые смежные классы

Пример:

Пример:

1. по
   
   
2. по
   Смежные классы по
3. 
   
   
   
   Группа не абелева, но левые смежные классы правым смежным классам
4. число остающееся на месте
   
   
   Левые смежные классы
   Правые смежные классы
   корме

Нормальная подгруппа для любого

Пример:

3. т.к. - абелева

Лемма

Пересечение нормальных подгрупп снова нормальная подгруппа

индекс

Лемма

Любая подгруппа индекса 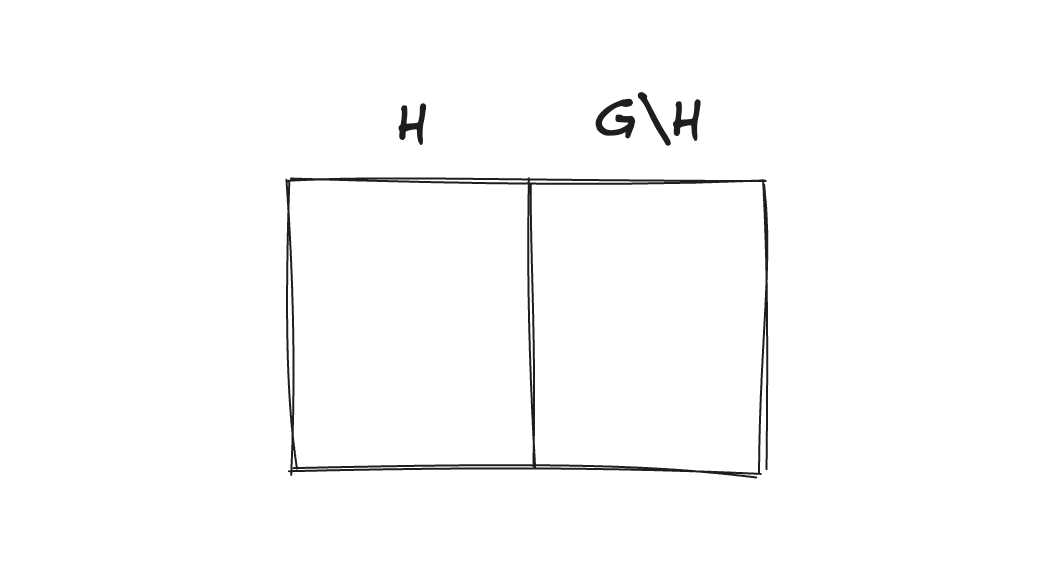нормальна

Теорема

Тогда след. условие эквивалентности

3. 
   Для любых

Доказательство

- сопряжение - сопрягающий элемент

Следствие (критерий нормальности подгруппы)

Пример:

1. 
   
   
   
2. 
   
   
   
   

Теорема

Описание сопряжённости в

Доказательство

Надо показать, что

Доказательство слишком построено на интуиции, чтобы качественно изложить его здесь