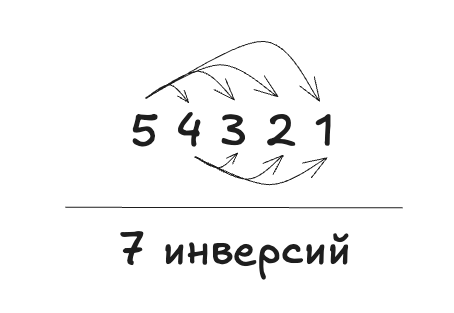
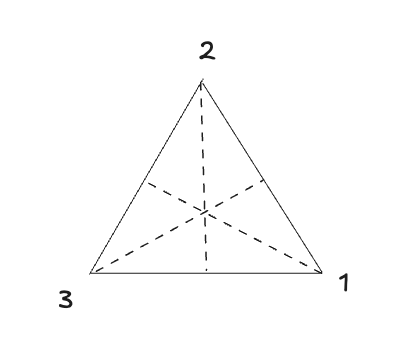
Примеры "возведения в степень":

Определим (в мультипликативной нотации)

Определим кратные

Наименьшее натуральное

3. - нейтральный элемент

Группа является своей подгруппой

Пример:

4. (повороты, диедральная)

=

Пример:

кол-во натуральных чисел и взаимно простых с ним - функция Эйлера

Группа перестановок

- , -

Пример:

Вывод: перестановки не коммутативны в контексте композиции

(в данном случае)

Порядок группы -

- -цикл (цикл длины ) если

Цикл длины - транспозиция

цикл - тривиальный цикл

-цикл - длинный цикл

- исходя из биективности и замкнутости - из-а транзитивности, рефлексивности и симметричности

Пример:

1. Любая перестановка раскладывается на произведение независимых циклов и это произведение единственно с точностью до порядка циклов
2. Независимые циклы коммутируют

Каждой орбите соответствует цикл

Пусть: -
- определение орбиты (цикла)

Записи перестановок

- полная запись

- цикленная запись

Цикленная запись

Пример:

Вывод: зависимые перестановки не коммутируют

Лемма

Любая перестановка раскладывается в произведение транспозиций

Доказательство:

Альтернативный пример:

- общая транспозиция

Инверсия

- образуют инверсию (беспорядок) если:

Пример:

* - количество инверсий

Пример:

четная перестановка

- фундаментальная транспозиция

Демонстрация нечётности:

Меняем и местами за фундаментальных транспозиций
() - фундаментальных транспозиций () - фундаментальных транспозиций

Вывод: любая перестановка является произведением фундаментальных транспозиций

Лемма

Тождестеннвая перестановка имеет эксклюзивно чётный знак

- все чётные перестановки - точно нечётные перестановки - нечётная перестановка Если

Теорема в - число чётных перестановок совпадает с числом нечётных

- ?

- произведение фундаментальных транспозиций

Вывод:

Знакопеременная группа/группа чётных перестановок

Игра

Чтобы "16" вернулось на место, нужно чётное число шагов

Теорема: Любую перестановку из можно разложить на транспозиций где - число независимых циклов (в том числе тривиальных)

- декремент перестановки

Очевидно, тривиальные циклы можно не считать, т.к. они входят и в , и в

Пример:

четная перестановка

четная перестановка

Теорема о смысле декремента:

- наименьшее количество транспозиций, за которое можно разложить перестановку.

Доказательство:

Переход: умножаем на

1. 
   
2. один из в каком-то цикле есть -
3. в одном цикле -
4. в разных циклах -

Гомоморфизм

Лемма

Доказательство:

Пример гомоморфизма:

Пример изоморфизма: